Semaine de la science
 Distances dans le système solaire

Faisons un bond de près de cinq siècles dans le passé et observons le ciel. En utilisant les méthodes de Copernic, nous allons calculer les distances de deux planètes au Soleil.

1ère distance :
La planète Vénus est l'une des deux planètes inférieures (avec Mercure). Elle se déplace à l'intérieur de l'orbite terrestre. A sa plus grande élongation (écart angulaire maximal avec le Soleil), Vénus (V) forme avec la Terre (T) et le Soleil (S) un triangle rectangle. Depuis la Terre on mesure cet angle : environ 46°.

  • Calcule l'angle VST

  • Exprime cos S dans le triangle TSV

  • Si la distance TS vaut 149 600 000 km, tu peux en déduire la distance VS de Vénus au Solei

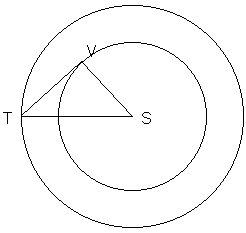2ème distance :
La planète Mars est une planète supérieure. Nous constatons qu'elle est en opposition avec le Soleil (Mars-Terre-Soleil sont alors alignés dans cet ordre) le 3 avril. Nous devons attendre le 18 juillet pour observer la quadrature (Mars, Terre et Soleil forment alors un triangle rectangle).

  • Combien de jours se sont écoulés ?

  • La Terre parcourt son orbite en 365 jours et Mars en 687 jours. De quel angle TST'a tourné la Terre pendant la période du 3 avril au 18 juillet ?

  • De quel angle MSM'a tourné Mars ?

  • On peut en déduire l'angle M'ST'

  • Utilisons le cosinus de cet angle dans M'ST' pour trouver la distance M'S Mars-Soleil